8. Computing Limits

c. Sandwich Theorem

1. The Theorem

The tricks covered on the previous page cover most limits involving .

A generalized polynomial is a sum of terms each of which is a coefficient times the variable to a numerical power, not necessarily non-negative integers. If all the powers are non-negative integers, then it is a polynomial.

However, if the limit involves other functions (such as exponential or trig functions), then there is one more technique that may prove useful, the Sandwich Theorem, which is also called the Pinching Theorem or the Squeeze Theorem. It is based on a simple fact:

If \(\displaystyle \lim_{x\to a}f(x)\) exists and \(\displaystyle \lim_{x\to a}g(x)\) exists and \[ f(x) \le g(x) \quad \text{for all} \quad x\ne a \] then \[ \lim_{x\to a}f(x) \le \lim_{x\to a}g(x) \]

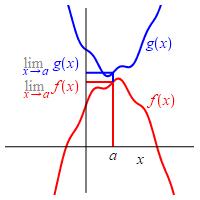
There are two wiggly curves. The curve f(x) wiggles as it goes from left to right with a maximum somewhere near x = a. The curve g(x) wiggles as it goes from left to right with a minimum somewhere near x = a. The f(x) curve always stays above the g(x) curve.
\(f=1-x^2+.2\sin(2\pi x)\)
\(g=1.2+x^2+.2\sin(2\pi x)\)

From this we have:

If \(\displaystyle \lim_{x\to a}g(x)\) exists and \(\displaystyle \lim_{x\to a}h(x)\) exists and \[ \displaystyle \lim_{x\to a}g(x)=\lim_{x\to a}h(x)=L \] and further: \[ g(x) \le f(x) \le h(x) \quad \text{for all} \quad x\ne a \] (i.e. \(f(x)\) is sandwiched between \(g(x)\) and \(h(x)\)) then \(\displaystyle \lim_{x\to a}f(x)\) exists and \[ \lim_{x\to a}f(x)=L \]

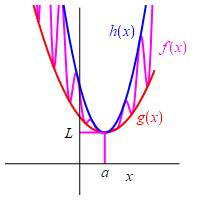
The plot shows two parabolas open upward which touch at their vertex at x = a. The upper parabola is labeled h of x. The lower parabola is labeled g of x. Between them, there is a wiggly curve labeled f of x.
\(g=1+x^2\)
\(h=1+3x^2\)
\(f=1+2x^2\sin(1/x)\)

Applying the previous proposition twice, we have that since \(g(x) \le f(x) \le h(x)\), then \[ \lim_{x\to a}g(x) \le \lim_{x\to a}f(x) \le \lim_{x\to a}h(x) \] We substitute \(\displaystyle \lim_{x\to a}g(x)=\lim_{x\to a}h(x)=L\) to get \[ L \le \displaystyle\lim_{x\to a}f(x) \le L \] Thus, \(\displaystyle\lim_{x\to a}f(x)=L\).

The formal proof appears in the chapter on Precise Limits and Continuity.

Let's start with a couple of examples which can also be computed by previous techniques.

Use the Sandwich Theorem to compute \(\displaystyle \lim_{x\to0}\dfrac{3x^2}{x+2}\).

This limit can easily be seen to be \(0\) by dividing the numerator and denominator by \(x\) which is the largest term in the denominator. However, we are asked to use the Sandwich Theorem.

To compute a limit as \(x\) approaches \(0\) we only need to look at \(x\)'s close to \(0\). So let's assume: \[ -1 \lt x \lt 1 \] and build up our function, \(\dfrac{3x^2}{x+2}\), in the middle. Add \(2\) to all sides: \[ 1 \lt x+2 \lt 3 \] Take the reciprocals, which reverses the inequalities: \[ 1 \gt \dfrac{1}{x+2} \gt \dfrac{1}{3} \] Multiply through by \(3x^2\) which is positive and so does nothing to the inequalities: \[ 3x^2 \gt \dfrac{3x^2}{x+2} \gt \dfrac{3x^2}{3}=x^2 \] So our function, \(\dfrac{3x^2}{x+2}\), is squeezed between \(x^2\) and \(3x^2\). Since: \[ \lim_{x\to0}(x^2)= \lim_{x\to0}(3x^2)=0 \] we conclude: \[ \lim_{x\to0}\dfrac{3x^2}{x+2}=0 \] also, by the Sandwich Theorem.

The solution to the following example shows how a mathematician would think through such a problem. Study it carefully!

Use the Sandwich Theorem to compute \(\displaystyle \lim\limits_{h\to 0}\dfrac{(1+h)^{1/5}-1}{h}\).

This limit can also be done by multiplying and dividing by the generalized conjugate \(1+(1+h)^{1/5}+(1+h)^{2/5}+(1+h)^{3/5}(1+h)^{4/5}\). However, we are asked to use the Sandwich Theorem.

Suppose the limit does have a value \(L\): \[ \lim\limits_{h\to 0}\dfrac{(1+h)^{1/5}-1}{h}=L \] Then for small \(h\) we have an approximate equality: \[ \dfrac{(1+h)^{1/5}-1}{h}\approx L \] We rearrange to obtain \[ (1+h)^{1/5}\approx 1+hL \] We raise both sides to the \(5^\text{th}\) power: (The coefficients come from Pascal's triangle.) \[ 1+h\approx (1+hL)^{5} =1+5Lh+10L^{2}h^{2}+10L^{3}h^{3}+5L^{4}h^{4}+L^{5}h^{5} \] To make the two sides agree, at least to first degree, we need \(L=\dfrac{1}{5}\). We now believe the limit is \(L=\dfrac{1}{5}\), but that does not mean we have proved it. For that we need the Sandwich Theorem. And for that, we need upper and lower bounds. We start with the equation \[ \left(1+\dfrac{1}{5}h\right)^{5}=1+h+\dfrac{2}{5}h^{2}+\dfrac{2 }{25}h^{3}+\dfrac{1}{125}h^{4}+\dfrac{1}{3125}h^{5} \] For small \(h\), the term \(\dfrac{2}{5}h^{2} \gt 0\) and the higher powers are smaller. We conclude: \[ \left(1+\dfrac{1}{5}h\right)^{5} \gt 1+h \] Turning this around and taking the \(5^\text{th}\) root gives: \[ (1+h)^{1/5} \lt 1+\dfrac{1}{5}h \qquad \qquad (*) \] Subtracting \(1\) and dividing by \(h\) gives: \[ \dfrac{(1+h)^{1/5}-1}{h} \lt \dfrac{\left( 1+\dfrac{1}{5}h\right) -1}{h} =\dfrac{1}{5} \] This is the upper bound (the upper crust) for our Sandwich Theorem.

We now need a lower bound. We need to change the \(1+\dfrac{1}{5}h\) in (*) to something smaller than \((1+h)^{1/5}\) without messing up the linear term \(\dfrac{1}{5}h\). So we try \(1+\dfrac{1}{5}h-h^{2}\). As above, we work out the \(5^{\text{th}}\) power: \[ \left( 1+\dfrac{1}{5}h-h^{2}\right)^{5} =1+h-\dfrac{23}{5}h^{2}-\dfrac{98}{25}h^{3}+(\text{higher degree terms}) \lt 1+h \] This is less then \(1+h\) because the quadratic term is negative. Turning this around and taking the \(5^{\text{th}}\) root gives: \[ (1+h)^{1/5}>1+\dfrac{1}{5}h-h^{2} \] Subtracting \(1\) and dividing by \(h\) gives: \[ \dfrac{(1+h)^{1/5}-1}{h}>\dfrac{\left(1+\dfrac{1}{5}h-h^{2}\right) -1}{h} =\dfrac{1}{5}-h \] This is the lower bound (the lower crust) for our Sandwich Theorem.

Consequently, we have the sandwich inequality: \[ \dfrac{1}{5}-h \lt \dfrac{(1+h)^{1/5}-1}{h} \lt \dfrac{1}{5} \] Since \(\displaystyle \lim\limits_{h\to 0}\left(\dfrac{1}{5}-h\right) =\lim\limits_{h\to 0}\dfrac{1}{5}=\dfrac{1}{5}\) we conclude \[ \lim\limits_{h\to 0}\dfrac{(1+h)^{1/5}-1}{h}=\dfrac{1}{5} \]

The following exercise is much easier than the previous examples. This limit involving a trig function cannot be done by previous techniques.

Compute \(\displaystyle \lim_{x\to0}x\cos\left(\dfrac{1}{x}\right)\).

Start with: \[ -1 \le \cos\left(\dfrac{1}{x}\right) \le 1 \]

\(\displaystyle \lim_{x\to0}x\cos\left(\dfrac{1}{x}\right)=0\)

As \(x\) approaches \(0\), \(\cos\left(\dfrac{1}{x}\right)\) oscillates between \(1\) and \(-1\) faster and faster; it is oscillatory divergent. However, when we multiply by \(x\), the result is different. Unfortunately, there is no way to simplify the \(\cos\left(\dfrac{1}{x}\right)\). So we turn to the Sandwich Theorem.

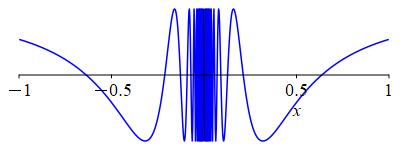
The plot shows a function which approaches y = 1 as x approaches plus or minus infinity but wiggles faster and faster between y = 1 and -1 as x approaches 0 from both sides.

We need to find upper and lower bounds on \(x\cos\left(\dfrac{1}{x}\right)\) whose limits we can compute. We start with the bounds on \(\cos\): \[ -1 \le \cos\left(\dfrac{1}{x}\right) \le 1 \] and multiply through by \(x\): \[ -x \le x\cos\left(\dfrac{1}{x}\right) \le x \]

So \(x\cos\left(\dfrac{1}{x}\right)\) is squeezed between \(-x\) and \(x\). Since: \[ \lim_{x\to0}(-x)= \lim_{x\to0}(x)=0 \] we conclude: \[ \lim_{x\to0}x\cos\left(\dfrac{1}{x}\right)=0 \] also, by the Sandwich Theorem.

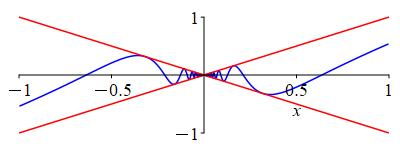
The plot shows two lines with slopes 1 and -1. In addition there is a function between them which wiggles faster and faster between y = x and -x as x approaches 0 from both sides.

On the next page, we will look at several very important limits involving trig functions, including \(\displaystyle \lim_{x\to0}\dfrac{\sin x}{x}\), where the application of the Sandwich Theorem is much more intricate.

© MY Math Apps

Supported in part by NSF Grant #1123255

NSF logo